Create a programming language

Python is a high-level language. It should be first interpreted into bytecode by interpreter written by C, and then translated into machine learning to be executed.

A powerful form of abstraction is to define a new language that is tailored to a particular type of application or problem domain.

A programming language has:

Syntax: The legal statements and expressions in the language
Semantics: The execution/evaluation rule for those statements and expressions

For example, if now we want to create a language called “Calculator”. We need to define:

Syntax:
1. The Calculator language has primitive expressions and call expressions. (That’s it!)
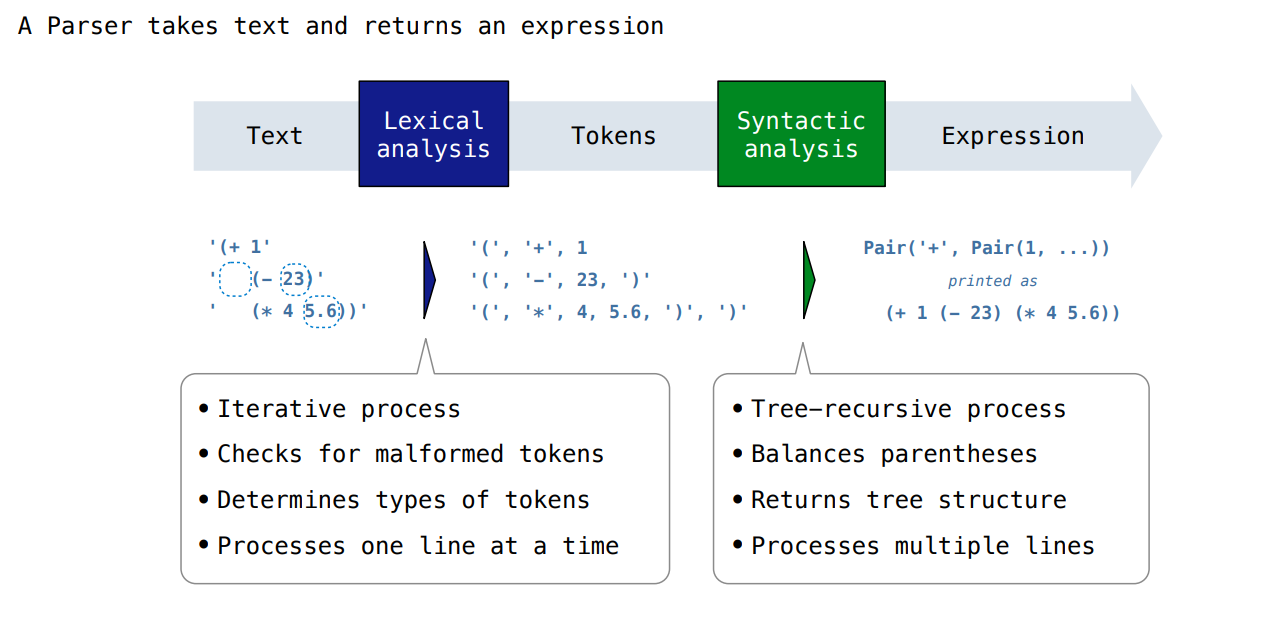
2. A primitive expression is a number: 2 -4 5.6; A call expression is a combination that begins with an operator (+, -, *, /) followed by 0 or more expressions: (+ 1 2 3) (/ 3 (+ 4 5)) 17
3. Expressions are represented as Scheme lists (Pair instances) that encode tree structures.
Senmantics: The value of a calculator expression is defined recursively.
- Primitive: A number evaluates to itself.
- Call: A call expression evaluates to its argument values combined by an operator.
  - +: Sum of the arguments
  - *: Product of the arguments
  - -: If one argument, negate it. If more than one, subtract the rest from the first.
  - /: If one argument, invert it. If more than one, divide the rest from the first.

To create a new programming language, you either need a:

Specification: A document describe the precise syntax and semantics of the language
Canonical Implementation: An interpreter or compiler for the language

Interpreter

So now let’s create an interpreter for Calculator.

Structure of Interpreter

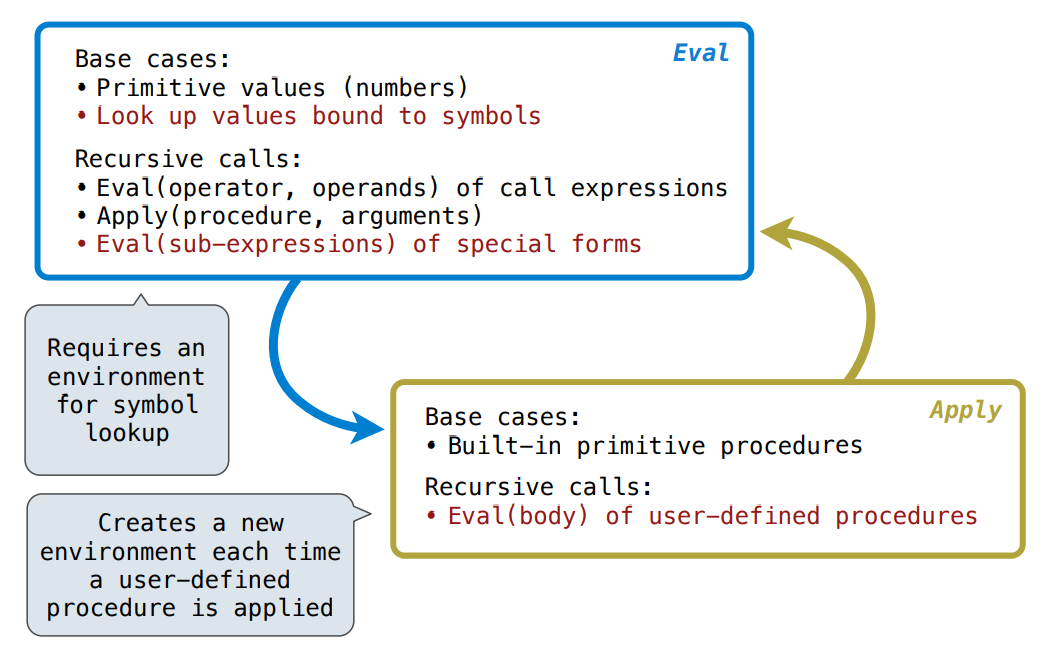
As we use eval to evaluate expressions in python interpreter, we define a calc_eval as below:

def calc_eval(exp):
    if isinstance(exp, (int, float)):
        return exp
    elif isinstance(exp, Pair):
        return calc_append(exp.first, exp.rest.map(calc_eval))
    else:
        raise TypeError
def calc_apply(operator, args):
    if operator == '+':
        return reduce(add, args, 0)
    elif operator == '-':
        return reduce(sub, args, 0)
    elif operator == '*':
        return reduce(mul, args, 1)
    elif operator == '/':
        return reduce(truediv, args, 1)
    else:
        raise TypeError
def reduce(fn, lst, initial):
    for item in lst:
      initial = fn(initial, item)
    return initial

# interactive interpreter
@main
def read_eval_print_loop():
    """run a read-eval-print loop for Calculator"""
    while True:
        try:
            src = buffer_input()
            while src.more_on_line:
                expression = scheme_read(src)#parsing
                print(calc_eval(expression))#evaluation
        except (SyntaxError, TypeError, ValueError, ZeroDivisionError) as err:
            print(type(err).__name__, ":", err)
        except (KeyboardInterrupt, EOFError):
            print('Calculation completed.')
            return

Special forms

Calculate is a simple example, which only includes a very small part of Scheme. How do interpreters process special forms in Scheme?

Special forms are identified by the first list element, like:

(if <predicate> <consequent> <alternative>)
(lambda (<formal-parameters>) <body>)
(define <name> <expression>)

Any combination that is not a known special form is a call expression.

Parsing

The task of parsing a language involves coercing a string representation of an expression. to the expression itself.

References

Interpreters

Interpreters